モンテカルロ法（円周率の近似_Python）

■モンテカルロ法の試し。
数学・アルゴリズム関連のテーマをChatGPTで聞いたらモンテカルロ法での円周率の近似が出てきた。少し調べると、一様分布の点をプロットして、それが円内に入っているか（下の式を満たすか）を判断して、入った数とプロット数から円周率を求めている。

モンテカルロ法のメインとなるコードが下。

import random
import math
import matplotlib.pyplot as plt

# 最大サンプル数と1ステップあたりの増分
（途中省略）

# 動的更新ループ
while total_count < N_MAX:
    for _ in range(STEP):
        x = random.uniform(-1, 1)
        y = random.uniform(-1, 1)
        total_count += 1

        if x * x + y * y <= 1.0:
            inside_x.append(x)
            inside_y.append(y)
            inside_count += 1
        else:
            outside_x.append(x)
            outside_y.append(y)

    pi_est = 4 * inside_count / total_count

    # データ更新
    sc_inside.set_offsets(list(zip(inside_x, inside_y)))
    sc_outside.set_offsets(list(zip(outside_x, outside_y)))

（以下省略）

実行結果が下。青の点が円の外にプロットされるもの、橙が円の内。プロットした点の数から近似値を計算して結果を表示。

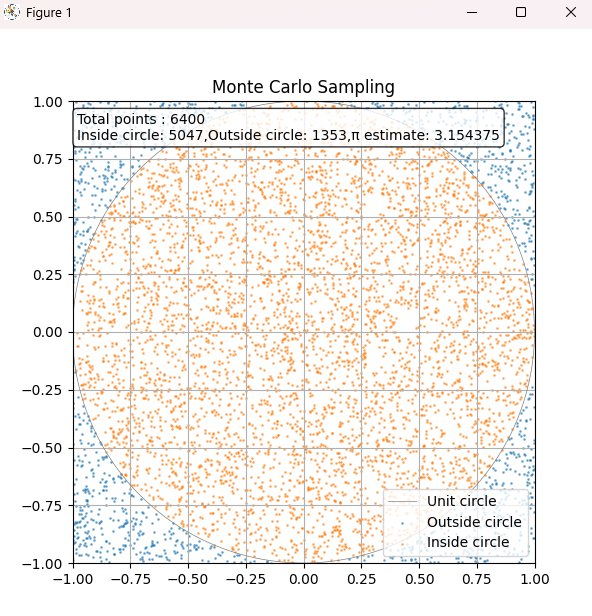
この近似値がどのくらい近いか、グラフにしたものが次。
横軸が試行回数N、縦軸が近似値（近似値が青、真値3.141592...が赤の点線）。ここでは最終的に1億2000万のプロットを行っている。

数千万にしてもそこまで真値に収束する感じでないけど、誤差については、1桁精度を増やすために100倍の回数が必要とのこと。1億の試行で少数4桁程度の精度で正しいらしい。
これをReactとかでも作ってみて、プログラムの重さとか見てみたい。